50年 前 に 出 版 された 理論電磁気学 砂川重信 著 大阪大卒→東北大教授→阪大教授
40年 前 に 出 版 された 電磁気学 二村忠元 著 京大卒→慶城帝国大学 助教授→東北大教授 恩 師
これらの 著 書 の中 の ローレンツ 変 換 は 理 解 できない 箇 所 がありました
ところが 最近 ( 2013 年 ) 出 版 された 高校数学でわかる 相対性理論 では 具体的 に、丁 寧 に 説 明 されております
素 人 に 理 解 できるように 工 夫 されています
長年 追いかけてきた 特殊相対性理論 が 80 才 過 ぎ た 今 頃 ようやく ほぼ 理 解 できました
特殊相対性理論 は アインシュタイン が 1905 年 に 発 表 した 4 っ の 論 文 の 中 の 一 つ です
発 表 当 時 は 世 界 の 科学者 も 理 解 できず、半 信 半 疑 だったそうです
従って、 アインシュタイン が ノーベル 賞 を 受 賞 したのは 同 年 に 発 表 された 【 光 量 子 仮 説 】 でした
アインシュタイン は 1905年 の 【 特殊相対性理論 】 に 続いて 10年後 の 1915年 に 【 一般相対性理論 】 を 発 表 した
特殊相対性理論 が 光 に 関する 論 文 一般相対性理論 は 重 力 に 関する 論 文
アインシュタイン 方 程 式 G μ ν + Λ g μ ν = ( 8 π G / c 4 ) / μ ν
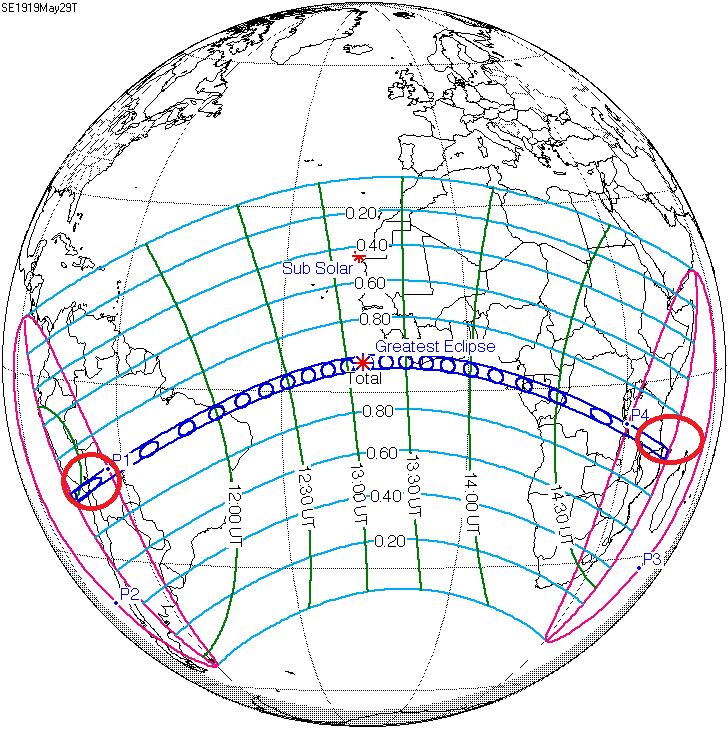

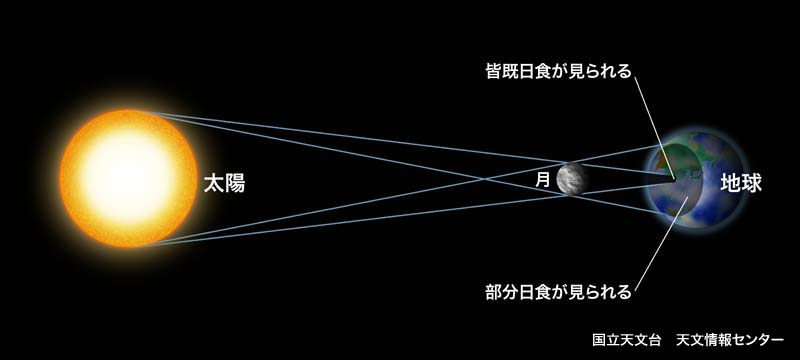
1919 - 5 - 29 の 皆 既 日 食
この皆既日食は、アルベルト・アインシュタインの 一般相対性理論 が正しいことを 実 証 した 日 食 として有名である。
特に プリンシペ島 で アーサー・エディントン が 行った 観 測 が 有 名 である。
プリンシペ島は、最大食を迎える地点からわずか 33 km と 条件のいい場所にあるためである。
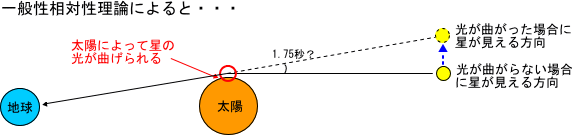
一般相対性理論によれば、重力場によって時空がゆがむと、そこを通過する 光はそのゆがみに沿って曲がる 。
これを観測者からみれば、見かけ上 光 源 の 位 置 がずれているように見える。
これは、重力がまるで凸レンズの役目を果たすことから重力レンズ効果と呼ばれている。
理屈上は、太陽のすぐそばを掠めるようにやってきた恒星の光も曲げられ、見かけの位置がずれているように見えるはずである。
しかし、太陽は極めて明るいため、そばにある恒星を観測するには、太陽が暗くなる皆既日食しかないのである。
理論上、1.75秒というわずかなずれが発生する。これは、ニュートン力学で予測されるずれの2倍である。
観測の結果、1.61秒というずれが観測され、一般相対性理論とニュートン力学で、一般相対性理論の方がより正しい値を予言したことから、
一般相対性理論 が 正しい という 結 論 となった。
また、ブラジルではアンドリュー・クロンメリンが同じく重力レンズ効果の観測を行った。
● G P S ( Gloval Positioning System ) と 相 対 性 理 論
自動車などの位置をリアルタイムに測定表示するカーナビゲーションシステムはグローバル・ポジショニング・システム (GPS) を
利用しており、GPS衛星に搭載された原子時計に基づき生成される航法信号に依存している。
GPS衛星からの信号を受信する装置では、さまざまな要因による補正を行うが、GPS衛星の時計との同期に関するものとして、
地表に対して高速で運動するGPS衛星の、特殊相対論効果による地表からみた時間の遅れ、
および地球の重力場による地上の時間の遅れ、言い換えれば一般相対論効果による衛星の時計の進みが含まれる[注 11]。
GPS衛星の 軌道速度は 秒速 約 4キロメートル と 高速であるため、特殊相対論によって時間の進み方が遅くなる。
一方、GPS衛星の高度は 約 2 万 キロメートルで、地球の重力場の影響が小さいことから、
一般相対論 によって 地 上 よりも 時 間 の進 み 方 が 速くなる。このように特殊相対論と一般相対論で互いに逆の効果をもたらすことになる。
この 相対論的補正 をせずに 1日 放 置 すると、位置情報が 約 11キロメートル もずれてしまうほどの時刻差になることから、相対論的補正は
GPS システム の 運 用 に 不可欠 である[8]。
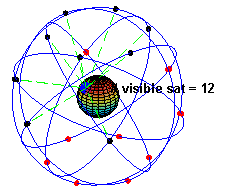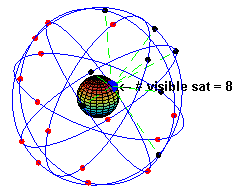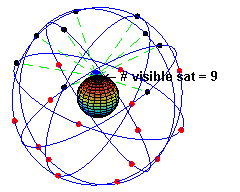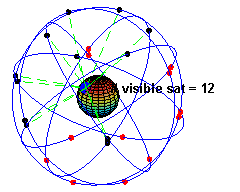

G P S の 原子時計 は 一 秒 間 が 100 億 分 の 4.45 秒 遅 く なるように 補 正 それていjいます
G P S 衛 星 は 現 在 世 界 米 国 32 ロシア 24 E U 4 中国 16 合 計 76 基 が 打ち上げ られています
尚 、 日本 の 準 天 頂 衛 星 ですが 、 これは 全地球 を カバー しているものでは な く、
日 本 と オーストラリア の 近 辺 だけ を 対 象 にしているので " Global " ではありません
このような " Local " な 衛星航法 システム は RNSS ( Regional Navigation Satellite System ) と いわれ ま す
ーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーーー
高校数学 でわかる 相対性理論 竹 内 淳 著
この 参考書 での ローレンツ 変 換 は やさしく 説 明 してあるので 他 の 参考書 で 理 解 できなかった
部 分 が 理 解 できました メ モ がわりに 抜 き 書 き しておきました
● 線 形 と 非 線 形 にいての 説 明
ま ず 、 線 形 と は 文 字 どうり 直 線 の こ と 例えば 一 次 式 y = a x + b
非 線 形 と は 線 形 で ないこと 曲 線 例えば 二 次 式 y = a x 2 + b x + c
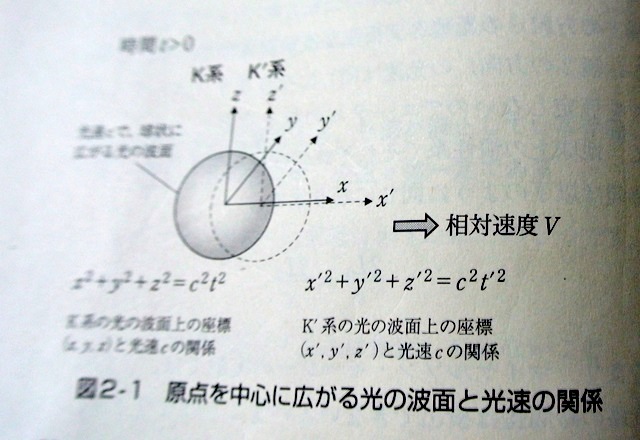
上 図 で 慣 性 系 K と K ´ K ´ は x 軸 方 向 に 速 度 V で 移 動 していると す る
t = 0 で 両 者 の 原 点 は 一 致 し、この 時 原 点 におかれた 光 源 から 光 が 放 射 されたと します
こ の 光 は 原 点 から まわりに 放 射 状 ( 球 状 ) に 広 がって いきます
慣性系 K の 時 間 t での 光 の波 面 の 座 標 ( x 、 y 、z ) で 表 す と、 原 点 からの 距 離 は
√ ( x 2 + y 2 + z 2 ) で す
光 速 を c とすると、 こ の 距 離 は c t に 等しい ので
√ ( x 2 + y 2 + z 2 ) = c t ( 2 . 1 ) となります
両 辺 を 2 乗 して 左 辺 に まとめると
x 2 + y 2 + z 2 - c 2 t 2 = 0
光速一定 の 原 理 の 要 請 から 、慣性系 K ´ においても K 系 と 同 じ く 光 は 高 速 c で
原 点 のまわりに 広 が って いきます
よって K ´ での 時 間 t ´ での 光 の 波 面 の 座 標 を ( x ´ 、 y ´ 、 z ´ ) とすると 、 前式 と 同 じ 形
の
x´ 2 + y´ 2 + z´ 2 - c 2 t´ 2 = 0 ( 2 . 2 ) という 式 がなり立ち ます
こ の 2 つ の 座 標系 の それぞれの 原 点 に 立っている 人 ( 例えば A さん と A´さん ) から 見 れ ば、
時 間 t = 0 で 放 射 された 光 が 原 点 から 球 状 に 広 がっていく 様 子 を ともに 見ている ことになります
図 2-1 で 、A さん が みているのが 実 線 の 波 面 で 、A´が さん が みているのが 点 線 の 波 面 です
こ の 2 つ の 座標系 の ( x 、 y 、z ) と ( x ´ 、 y ´ 、 z ´ ) の 間 にどのような 関 係 があるのか を
明 ら か に すること です
慣性系 K ´ は x 軸方向 に 動 いてる ので 、 y 座標 や z 座標 については この 2 つ の 系 で差 はありません
よって y = y ´ ( 2 . 3 ) z = z ´ ( 2 . 4 ) です
とすると それ 以 外 の 変 数 である x t と x ´ t´ の 関 係 を 調 べ れば よ い ことに なります
この 場合 、 座標変換 を 表す 式としては 、 x ´ が x と t の 関 数 f ( x 、 t ) として あらわされ、
t´ が x t の 関 数 g ( x 、 t ) して 表せる でしょう
x ´ = f ( x 、 t ) ( 2 . 5 ) t´ = g ( x 、 t ) (
2 、.6 )
◆ 座 標 変 換 が 1次式 で 表せなければ いけない 理 由
例えば、 x と t が 2 次 の 式 ( x や t の 2 乗 の 項 が ある 式 )
と して 表 される 簡 単 な 例 として
x ´ = A x 2 ( 2 . 7 )
という 場 合 を 考えて みましょう について 解 く と
x = √ ( x ´ / A ) ( 2 . 8 ) となります
この 式 が 座標変換 を 表す 式 として 妥 当 か どうか 、考えて みましょう
慣性系 K か ら K´系 を 見 た 場 合 と 、 慣性系 K ´ か ら K を 見 た 場 合 の 座標変換 の 式 は
同 じ 形 になるだろう ということ は 直 感 的 に わかります
K´系 は K 系 に 対 して 速 さ V で x 方向に動いているわけですから、
これは K´系 から 見れば、 K 系 は x 軸 の負 の 方向 に速 さ V で 動いているように 見えるわけです
見え方 の 違いは、 相手 が 相対速度 + V で 動 いている ように見えるか、 - V で 動いているように
見えるかの 違 い しか ないわけです
従って、 ( 2 . 5 ) 式 と ( 2 、.6 ) 式 の 変換式 が 成り立つ としたら、その 逆 の
x = h ( x´ 、 t´ ) ( 2 . 9 )
t = k ( x´ 、 t´ ) ( 2 . 10 )
も 成り立つ はずでり 、しかも、 f ( x 、 t ) と h ( x´ 、 t´) はともに 似 た 形 になるはずです
同 様 に t´ = g ( x 、 t ) と t = k ( x´ 、 t´ ) も 似 た 形 になるはずです
両 者 の 次 数 も 同 じ に なるでしょう
こ の 認 識 の もとに 、 ( 2.8 ) 式 を 見 る と、右辺の はルートの中に入っていて、
( 2.7 ) 式 の 2次 式 と は まったく 異 な る ことが わかります
1次式を用いた場合にのみ 次数 が 一致する
よって ローレンツ 変 換 は 1 次 の 式 ( 線 形 ) 表 せ ら れ る ことが わかります
● ローレンツ 変 換 座 標 変 還 式 を 求 め る
1次式のみが許されるということがわかったので、
( 2.5) 式 と ( 2.6 ) 式 の 座 標 変 換 を 次 の 2 つ の 1 次 式
x ´ = A x + B t ( 2 . 11 )
t´ = Q x + R t ( 2 . 12 ) で 表 す ことに しましょう
慣性系 K´ は K 系 に 対 して 速 さ V で x 方 向 に 進んでいる ので、
慣性系 K の 座 標 上 で の 原 点 は x = V t で表されます
一方、 慣性系 K´ の 原点は 慣性系 K´ の座標として x ´ = 0 の まま です
よって この 両者を ( 2 . 11 ) 式 に代入すると
0 = A V t + B t = ( A V + B ) t
B = - A V となります
これで 未知の係数が一つ減りました ( 2 . 11 ) 式 に代入すると
x ´ = A x - A V t ( 2 . 11 ´ )
t´ = Q x + R t ( 2 . 12 ´ ) となります
( 2 . 2 ) 式 に ( 2 . 11 ´ ) 、 ( 2 . 12 ´ ) 、 ( 2 . 3 ) 、 ( 2 . 4
) 式 を 代入すると
0 = x´ 2 + y´ 2 + z´ 2 - c 2 t´ 2
= A 2 ( x - V t ) 2 + y 2 + z 2 - c 2 ( Q x + R t ) 2
= A 2 x 2 - 2 A 2 V x t + A 2 V 2 t 2
+ y 2 + z 2 - c 2 Q 2 x 2 - 2 c 2 Q R x t - c 2 R 2 t 2
= ( A 2 - c 2 Q 2 ) x 2 + y 2 + z 2
+( A 2 V 2 - c 2 R 2 ) t 2 - 2 ( A 2 V + c 2 Q R ) x t ( 2.13 )
となります これで 変 数 x 、y 、 z 、 t の 式 に なりました
変 数 x 、y 、 z 、 t の 間には ( 2.1) 式 が 成り立って いるので
( 2.1) 式を変形 し て y 2 + z 2 = - x 2 + c 2 t 2 と なるので
これを ( 2.13) 式 に 代入 して y と z を 消 去 します
( 2.13) 式 は 0 = ( A 2 - c 2 Q 2 - 1 ) x 2 + ( A 2 V 2 - c 2 R 2 + c 2 ) t 2 - 2 ( A 2 V + c 2 Q R )
この 式 は 任 意 の x や t に 対して 成り立つ 必 要 があるので、
それぞれの 係 数 は ゼ ロ でなければ ならない ことが わかります
A 2 - c 2 Q 2 - 1 = 0 ( 2.14 )
A 2 V 2 - c 2 R 2 + c 2 = 0 ( 2.15 )
A 2 V + c 2 Q R = 0 ( 2.16 )
こ の 3 つ の 式 が 得られます こ の 連立方程式 を 解 い て A Q R を 求めます
求め方は 中学 か ら高校数学程度 の 問題です 計算は 簡単なので 省 略 して 結 果 のみ 示します
A = R = 1 / 【 √ ( 1 - V 2 / c 2 ) 】 ( 2.23 )
Q = - V / c 2 【 1 / ( 1 - V 2 / c 2 ) 】 ( 2.24 )
式 を 簡 単 に するために β = V / c γ = 1 / √ ( 1 - β2 ) を 導 入 して
A = R = γ Q = - βγ/ c
これを 使 っ て ( 2.11 ) 式 と ( 2.12 ) 式 を 書 き 直 す と
x ´ = A x - A V t
= γ ( x - c βt ) ( L - 1 )
= ( x - v t ) / √ ( 1 - v 2 / c 2 )
t´ = Q x + R t
= γ ( t - β / c ) ( L - 2 )
= ( t - v x / c 2 ) / √ ( 1 - v 2 / c 2 )
これで 慣性系 K´ の 変 数 x´ と t´ が 、 慣性系 K の 変 数 x と t の 関 数 として 求められ ました
この 両式 で 表 せられる 変 換 を ローレンツ 変 換 と 呼 びます
★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★


