　　　np - 70

　　　★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★★
　　　　

　　　　　　　　　　　　　二点間の　距離　を求める公式（ 2次元、 3次元）

　　　　

$(x_1,y_1)$ と $(x_2,y_2)$ を結ぶ線分の長さは、
$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$

$(x_1,y_1,z_1)$ と $(x_2,y_2,z_2)$ を結ぶ線分の長さは、
$\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$

　　　　特に、点の片方が原点の場合をよく使います。その場合の公式は以下のようになります：

(x, y)

$(x,y)$ から原点までの距離は、

\sqrt{x^{2} + y^{2}}

$\sqrt{x^2+y^2}$

　　　　　　　　　具体例

例題１： $xy$ 座標平面上で $(3,4)$ と $(-2,0)$ を結ぶ線分の長さ $d$ を求めよ。

解答

例題２： $xyz$ 座標空間上で $(1,0,-2)$ と $(3,4,5)$ を結ぶ線分の長さ $d$ を求めよ。

解答

公式より、

d = \sqrt{(1 - 3)^{2} + (0 - 4)^{2} + (- 2 - 5)^{2}} = \sqrt{4 + 16 + 49} = \sqrt{69}

$d=\sqrt{(1-3)^2+(0-4)^2+(-2-5)^2}\\ =\sqrt{4+16+49}\\ =\sqrt{69}$

　　　　　　　　　　　　　証明（二次元平面の場合）

　　　　　二次元座標平面上の2点

A (x_{1}, y_{1})

$A(x_1,y_1)$ と

B (x_{2}, y_{2})

$B(x_2,y_2)$ の距離を計算してみましょう

　　　　　　　　　　　　　　

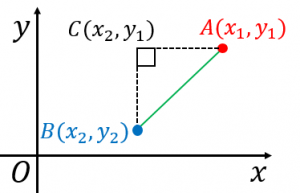
　　　　　　　　　　図のように点

C

$C$ を置いて、直角三角形

A B C

$ABC$ を作ってみます。

A C

$AC$ の長さは

| x_{1} - x_{2} |

$|x_1-x_2|$ となります。

（図では

x_{1} > x_{2}

$x_1 > x_2$ なので

A C

$AC$ の長さは

x_{1} - x_{2}

$x_1-x_2$ ですが、

x_{1} < x_{2}

$x_1 < x_2$ の場合も一緒に扱うためには絶対値が必要です。）

よって、三平方の定理を使うと

A B = \sqrt{A C^{2} + B C^{2}} = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2}}

$AB=\sqrt{AC^2+BC^2}\\ =\sqrt{(x_1-x_2)^2+(y_1-y_2)^2}$
となります。

　　　　　　　　　　　　　　　　　　　　　　証明　（三次元空間の場合）

　　　　　三次元座標空間上の2点

A (x_{1}, y_{1}, z_{1})

$A(x_1,y_1,z_1)$ と

B (x_{2}, y_{2}, z_{2})

$B(x_2,y_2,z_2)$ の距離を計算してみましょう。

　　　　　　　各辺が座標軸に平行な直方体で、

A, B

$A,B$ が頂点（のうちの2つ）になるようなものを作ってみます。

　　　　　　　　　　　　　　

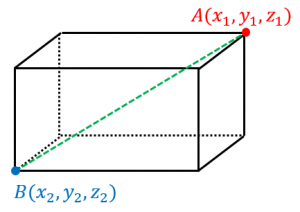
　　　　　　　　　　　平面の場合と同じ考え方により、3つの異なる方向の辺の長さはそれぞれ

| x_{1} - x_{2} |, | y_{2} - y_{2} |, | z_{1} - z_{2} |

$|x_1-x_2|,|y_2-y_2|,|z_1-z_2|$
　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　　　　　　　　　　　　　　　　　　　　　となります。

　　　　　　　　　　　　よって、直方体の対角線の長さを求める公式により、

A B = \sqrt{(x_{1} - x_{2})^{2} + (y_{1} - y_{2})^{2} + (z_{1} - z_{2})^{2}}

$AB\\ =\sqrt{(x_1-x_2)^2+(y_1-y_2)^2+(z_1-z_2)^2}$
　　　　　　　　　　　　　　　　　　となります。　　　